Tasks, Questions, and Practices

Bookmark

By Chandra Hawley Orrill, Posted May 11, 2015 – 

We know that to understand how our students think, we need to ask them good questions. We read all the time about the importance of questioning and different kinds of questions. But, all questions are not created equally. In this two-part blog entry, I want to explore the relationship among asking questions, the problems we use in our classrooms, and the effects questions and tasks have on our ability to address some of the Common Core’s Standards for Mathematical Practice (CCSSI 2010). Specifically, let’s think about these Standards of Practice:

SMP 1.   Make sense of problems and persevere in solving them

SMP 6.   Construct viable arguments and critique the reasoning of others.

SMP 3.   Attend to precision.

The goal of this blog post is to emphasize the point that the tasks you choose to use in your classroom enhance or inhibit your ability to ask the kinds of questions that allow students to develop these three Standards for Mathematical Practice (SMPs).

Tasks Matter

The cognitive demand of a task is the level of cognitive engagement needed to complete the task (Stein et al. 2009). You could think of a problem that requires only memorization as being at the low end of cognitive demand, whereas a task that requires students to make connections between and among mathematical ideas in new ways is a high cognitive demand task. Research has shown that using high cognitive demand tasks in ways that support that rigor will lead to increases in student learning.

Questions Matter

To maintain the level of cognitive demand written into a question, a teacher must ask good questions. A high cognitive demand question is one that invites students to explain their thinking, make new connections, describe their process, or critique other ideas. Questions that maintain high cognitive demand engage students in making more sense of the mathematics, whereas questions that lower the cognitive demand focus on correct answers and correct answer paths.

Standards of Practice Come from Tasks and Questions

One of the challenges of the Common Core is the need to address the SMPs all the time. We all know that students need to actually practice the SMPs to develop the skills and dispositions that are valued. Although forgetting about the SMPs is easy, they are crucial to students’ development as mathematical thinkers. For this discussion, I’ve chosen three SMPs to focus on because they are all closely related to tasks and questions.

•     High cognitive demand tasks require students to make sense of them. Unlike a page of simple number sentences, high cognitive demand tasks require that students read them, determine what the question is, and determine how to use the information provided in the task. Sometimes, this is also true of lower cognitive demand tasks.

•     High cognitive demand tasks often have multiple ways of finding an answer or multiple correct answers. When this is true, you and your students have much more to talk about. And many more student ideas come out in the conversation. All of this offers an opportunity to make sense of one another’s thinking and for each student to learn how to communicate about her or his own thinking.

•     When we engage in meaningful discussions of mathematics that feature a lot of different ideas, it becomes more and more important to be sure everyone in the room knows exactly what each person is talking about. Precision is developed by being asked to make sure everyone understands a viewpoint. It comes from the use of specific mathematical terms, from labeling answers, and from using representations as tools to support communication about mathematics.

Your Turn

Now it’s your turn to think about the effects of Tasks, Questions, and Practices. Consider the two tasks below.

1.   Decide which aspects of each task make them of higher or lower cognitive demand. Could you do anything to raise the cognitive demand of either task?

2.   Think about questions you could ask students as they work on these tasks. Are these questions raising or lowering the cognitive demand of the task?

3.   How does each task attend to perseverance and sense making?

4.   How does each task promote making viable arguments? What about critiquing the arguments of others?

5.   How does each task provide students with opportunities to communicate in precise ways about mathematics?

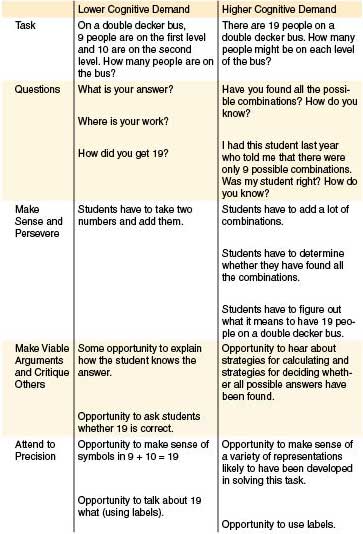
Task 1. Lunchroom Problem

 Ella would like to buy lunch in the lunchroom today. Meals cost $2.50. Dessert costs an extra 75 cents, and milk costs 75 cents. If Ella has $5.00, can she buy lunch in the lunchroom?  (Please See Chart at the bottom of this post.)

Task 2. Buying Lunch

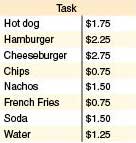
You are going to the amusement park. At the amusement park, you will buy lunch. You don’t want to carry coins, only dollar bills, because coins can fall out of your pocket on the roller coaster. You can purchase any of the items on the menu, but you cannot buy more than one of the same item, and you cannot spend more than $10.00. Using the menu to the left, find out how many different lunches you could buy without receiving any change back.

     

More Reading about Cognitively Demanding Mathematical Tasks

National Council for Teachers of Mathematics. 2014. Principles to Action: Ensuring Mathematical Success for All. Reston, VA: National Council of Teachers of Mathematics.

Common Core State Standards Initiative. CCSSI. 2010. Common Core State Standards for Mathematics (CCSSM). Washington, DC: National Governors Association Center for Best Practices and the Council of Chief State School Officers. http://www.corestandards.org/wp-content/uploads/Math_Standards.pdf

Stein, Mary Kay, Margaret Schwan Smith, Marjorie A. Henningsen, and Edward A. Silver. 2009. Implementing Standards-Based Mathematics Instruction: A Casebook For Professional Development, 2nd ed. New York: Teachers College Press.

Chandra Hawley Orrill, corrill@umassd.edu, is an associate professor and department chairperson in STEM Education and Teacher Development at the University of Massachusetts–Dartmouth. She teaches courses on mathematics content, like proportional reasoning and number sense, for teachers seeking their professional license as well as teaching a variety of courses in the Mathematics Education PhD program. Her interest is in how teachers understand the mathematics they teach and how we can better support teachers in understanding mathematics. She has conducted hundreds of hours of professional development focused on standards-based mathematics and on technology integration in mathematics for elementary school teachers.

This week, I chose to explore high cognitive demand tasks vs. low cognitive demand tasks.  I think it is important for children to make connections with the math they are doing.  The more the students make connections the more they will appreciate math and keep a growth mindset.  

When completing my assignment Problem Set#1, number 8 sparked my interest:  Identify the following task as a "low level" or a "high level" cognitive demand task.  If the task is considered a "low level" cognitive demand task, rewrite the task so it is a "high level" cognitive demand task.

Solve.  14+___=21

I determined it was a "low level" cognitive demand task, because it is strictly procedural.

I rewrote it:

Blake has merchandise to sell:

2 Salt Lamps

1 Lava Lamp

2 LED Light Bulbs

2 Regular Light Bulbs

Prices:

Salt Lamps cost $21 each

Lava Lamps cost $14 each

LED Light Bulbs cost $7 each

Light Bulbs cost $2 each

Blake sold $21 worth of merchandise.  One item sold was a lava lamp.  What did he sell with the lava lamp? (1 LED Light bulb)

Going further, I thought of expanding it.

What merchandise and how many of each remained after the $21 dollar sale?

(2 Salt Lamps, 1 LED Light Bulb and 2 Regular Light Bulbs)

In Blake's final sale, he sells all of the remaining merchandise.  How much money was needed to purchase all of the merchandise that was left?  ($53)

This week I chose to explore reviewing the concept of subtraction with children.  I like this because the materials needed are very basic.  The content of the lesson is nicely intertwined with children being able to group and classify foods based on similarities.  

I look forward to using this lesson in the future.  It's important to show that when adding numbers, the answer is the same and it doesn't matter which number comes first, but it does matter which number comes first.  

I think this is a good lesson that anyone could use and modify if needed, and adapt to another topic.  One example that comes to mind for me is using Valentine's Day themed pictures instead of food.  This could also lead into a follow up activity of the students pasting the pictures in a math themed book that they model subtraction with the pictures and write the equation on the page also.  

One of my goals of teaching math to children is to teach them common core aligned math  lessons and make it as interesting as possible for the children.  I want my students to develop a love and understanding for math as soon as they begin learning it.

Combining Foods

Unit:Food Pyramid Power
Grade: PreK to 2nd
Periods: 1
Author: Grace M. Burton

Materials

• Crayons
• Paper
• Pictures of food

Instructional Plan

To review the concept of subtraction, name two sections of the food pyramid (vegetables, fruits, meats, cereal and grains, and milk and dairy products). Place the students in pairs and assign one student in each pair to locate three to five pictures of food belonging to the fruit section.

Ask the other student to find three to five pictures of meat. Now ask the pairs to discuss the number of food pictures that they collected all together and to compare the number of pictures each student collected. Call on a volunteer pair to describe the compilation and the comparison of their pictures in words and in addition and subtraction sentences. Repeat with other pairs. Then name a difference, such as two, and have each pair model the meaning of the subtraction sentence by combining all their pictures and making two new sets of food pictures. Call on several groups to explain how they constructed sets with the given difference. Repeat, if you wish, with other differences.

Using six food pictures in one group and one food picture in another group, ask the students to dictate a set of related addition and subtraction sentences that describe the joining and comparison of these groups.

The sentences for these groups will be:

7 – 1 = 6 
7 – 6 = 1 
6 + 1 = 7 
1 + 6 = 7

Ask the students whether the order of the addends changes the sum. [It does not.] Then ask whether the order of the numbers matters in a subtraction sentence. [It does matter. Subtraction is not a commutative operation.]

Next, have the students make two groups of food pictures of any size that they choose as long as the sum of the groups is 12 or less. Then ask them to generate addition and subtraction sentences that can be modeled using the pictures in their groups. If the students seem comfortable with this procedure, encourage them to make other pairs of picture groups with a sum of their choice and then combine and compare the groups, writing equations to describe each action. This activity is designed to help them focus on the commutative property and on the relation of subtraction to addition. When all the students are ready, suggest that they make a set of seven pictures and a set of zero pictures and write the four related addition and subtraction sentences, as shown below:

7 – 7 = 0 
0 + 7 = 7 
7 – 0 = 7 
7 + 0 = 7

Then call the students together and ask a volunteer to make two sets. Call on a second student to write the two addition sentences, and ask a third volunteer to write the two subtraction sentences that the food picture groups suggest. You may wish to repeat this procedure with other trios of volunteers. Finally, invite one of the students to make two sets of food pictures, each containing three pictures. Call on a volunteer to write the related addition and subtraction sentences that use these sets. [These will be: 3 – 3 = 0 and 3 + 3 = 6.]

Finally, ask them to draw two of the groups that they made during this lesson and write number sentences that describe the combination and comparison of the groups. You may wish to add these recordings to their portfolios. These provide evidence of their growth in understanding of the important topics central to this lesson.

Assessments and Extensions

Assessment Options

At this point, you may wish to add more documentation to the Class Notes recording sheet. These notes will be valuable as you plan appropriate remediation and enrichment opportunities.

Extension

Move on to the last lesson, Try For Five.

Questions and Reflections

Questions for Students

1. If one group has seven food pictures and another group has two pictures, how many will there be in all? How many more pictures are in the larger group?
2. How many different addition and subtraction facts can I write if I make a group with five food pictures? How are the facts alike? How are they different?
3. Can you show that 2 + 4 and 4 + 2 have the same sum?
4. Suppose I make two groups each with four food pictures. What sentences will describe these groups?
5. How could you help a friend model with pictures of food the number sentence 5 + 4 = 9? How about 5 + 0 = 5?
6. How many addend pairs can you find for a sum of seven? What subtraction sentences do they suggest?

Teacher Reflection

• Which students easily used number sentences to record the combination of groups?
• Which students easily recorded comparisons with number sentences?
• Which students have some of the facts memorized?
• Did most students remember the effects of adding or subtracting zero?
• Which students were able to find all the members of a fact family?
• Which students are still having difficulty with the objectives of this lesson? What additional instructional experiences do they need?
• What will I do differently the next time that I teach this lesson?

 

Objectives and Standards

Learning Objectives

Students will:

• Model related addition and subtraction facts up to 12.
• Model the commutative property.
• Review the role of the additive identity.
• Generate fact families when they are given two addends.

Common Core State Standards – Mathematics

Pre K to 2nd

• Kindergarten
• CCSS.Math.Practice.MP4
  Model with mathematics.
• CCSS.Math.Practice.MP5
  Use appropriate tools strategically.
• CCSS.Math.Practice.MP6
  Attend to precision.

Pre K to 2nd

• Grade 1
• CCSS.Math.Practice.MP4
  Model with mathematics.
• CCSS.Math.Practice.MP5
  Use appropriate tools strategically.
• CCSS.Math.Practice.MP6
  Attend to precision.

Pre K to 2nd

• Grade 2
• CCSS.Math.Practice.MP4
  Model with mathematics.
• CCSS.Math.Practice.MP5
  Use appropriate tools strategically.
• CCSS.Math.Practice.MP6
  Attend to precision.

Common Core State Standards – Practice

• CCSS.Math.Practice.MP4
  Model with mathematics.

• CCSS.Math.Practice.MP5
  Use appropriate tools strategically.

• CCSS.Math.Practice.MP6
  Attend to precision.

Related Resources

	Sorting Foods Grade: PreK to 2nd Use the Food Pyramid to create sets of up to 10.
	Eating Patterns Grade: PreK to 2nd Sort, analyze, and extend patterns.
	Pyramid Power Grade: PreK to 2nd Explore relationships between numbers.
	Try for Five Grade: PreK to 2nd Explore ways to decompose numbers.

Exploring Pennies and Dimes

Unit:Number Cents 
Grade: PreK to 2nd
Periods: 1
Author: Grace M. Burton

Materials

• Plastic bags, each containing 24 pennies and 3 dimes
• Book: Alexander Who Used to Be Rich Last Sunday
• Paper and crayons
• Paper bags
• Ten Frame Activity Sheet
• Paper Bag Activity Sheet

Instructional Plan

Distribute plastic bags containing 24 pennies and 3 dimes to each child. To begin this unit, read Alexander Who Used to Be Rich Last Sunday. Then reread the book and ask the children to work with a friend to model the amounts he spends, starting with page 12 where he buys some bubble gum. [There will be enough money if children combine their bags of money.]

Hold up a penny and ask the children to find a penny in their bag. Ask them to describe the penny, and record their descriptions on chart paper. Now ask the children to place a piece of paper over one penny and to rub the paper with a crayon to make impressions of both sides of the coin. Ask them to record the coin’s value in both words (1 cent) and using the cent sign (¢). Then repeat the procedure with a dime.

Next ask the children what similarities and differences they notice about the coins. Then ask what words they used when they were talking about the money. As children name them, create a word wall by writing the words on a poster or on sticky notes and post them in a prominent place in the classroom.

Ten Frame Activity Sheet

Next give each child a copy of the Ten Frame Activity Sheet. Ask them to use it to find out how to trade the pennies in their bags for dimes. Model this by placing 1 penny in each cell of the ten frame, and when the frame is full, exchanging the 10 pennies for 1 dime. Then ask them to find out how many dimes’ worth of pennies they have in their bag. [You may wish to remind the children that both a number (such as 4) and a unit (such as dimes or cents) must be given to express a quantity.]

Write in a prominent place and call children’s attention to the cents sign (¢) and the word "cents". Now put the children into pairs, and give each pair a number cube and a paper bag. Ask the children to dump the coins from both their plastic bags onto a piece of paper. Then have the children take turns rolling the number cube, with one child rolling to tell how many dimes will be put into the paper bag, and the other child rolling to determine the number of pennies. After both children have rolled the number cube, ask them to record the amount they have in the bag in both formats and then to verify their prediction. Ask them to repeat the activity several times. Students should record the results on the Paper Bag Activity Sheet.

Paper Bag Activity Sheet

When the children are ready, ask for volunteers to choose one of the amounts they modeled and show it in coins to the other children. Then for a first entry for their portfolio, ask the children to write one amount and draw the coins which show that amount.

Assessments and Extensions

none

Questions and Reflections

Questions for Students

1. What words did we use today, which tell about money?

[Penny and dime.]

2. How many pennies do we trade for a dime?

[10.]

3. What is alike between a penny and a dime? What is different?

[They both are coins and are used as money; each size is different, and each value is different.]

4. How could you help younger child trade pennies for dimes?

[You could use a ten frame to show that 10 pennies have the same value as a dime.]

5. How would you model 23 cents? 32 cents?

[23 cents: 2 dimes and 3 pennies, 1 dime and 13 pennies, or 23 pennies]
[32 cents: 3 dimes and 2 pennies, 2 dimes and 12 pennies, 1 dime and 22 pennies, or 32 pennies.]

6. What two ways can you write "cents"?

[With a word or with a cents symbol.]

Teacher Reflection

• With which coin values were children familiar before the lesson began?
• Which students met all the objectives of this lesson? What extension activities would be appropriate for those students?
• Which students did not meet the objectives of this lesson? What instructional experiences do they need next?
• Were the children able to distinguish between the dime and the penny?
• Would you make any adjustments the next time you teach this lesson?

 

Objectives and Standards

Learning Objectives

Students will:

• Model amounts with pennies and dimes to 60 cents.
• Identify words and symbols relating to cents.
• Recognize physical differences in pennies and dimes.
• (This is lesson 1 of the Unit below from NCTM)

• Number Cents

  Grade: PreK to 2nd
  Author: Grace M. Burton
  In this unit, students explore the relationship between pennies, nickels, dimes, and quarters. They count sets of mixed coins, write story problems that involve money, and use coins to make patterns. 
  The unit consists of six lessons that give children an opportunity to identify individual coins and to make sets of coins with equivalent values. Students also pattern with coins, and use coins in real world situations. They will also determine the value of sets of pennies, nickels, dimes, and quarters, and record the value using 2 forms of notation. Actual coins are used in all lessons.  
  Numerous connections to children's literature are made in this unit. Suggestions for books dealing with money and coins are available.  
   A Sampling of Children's Books
  The lessons in this unit build an understanding of the relationship between coins in the United States monetary system and use coins in patterning, and in addition and subtraction situations. 

  Math Content 

  Students will: 
  • Exchange pennies, nickels, dimes, and quarters, model sets of coins which show a given amount. 
  • Use addition and counting to solve problems using money. 

  Lessons

  	Exploring Pennies and Dimes Grade: PreK to 2nd Model amounts to 60 cents.
  	How Many Ways? Grade: PreK to 2nd Extend your investigation of the previous day to include nickels.
  	Trading For Quarters Grade: PreK to 2nd Learn about quarters.
  	Modeling Prizes Grade: PreK to 2nd Model amounts to 70 cents.
  	Making Change Grade: PreK to 2nd Model prices mentioned in a children's book. Then, make change from a given amount by counting on from the price.
  	Looking Back and Moving Forward Grade: PreK to 2nd Review the work of the previous lessons; discuss and model prices and the words on the word wall, and play games to facilitate continuing practice.

  Objectives and Standards

  NCTM Standards and Expectations

  • Pre-K - 2

  • Number and Operations

  This week I chose to explore a unit on NCTM website, with focus on the first lesson.  I look forward to teaching students about money.  I especially like how the unit introduction includes literature and there is a suggested list of literature that goes with the unit.  
• One of the ideas I had was to use plastic replica coins and distribute different coins to students as a reward for participation.  The students could save these coins until the end of the unit at which the students would be able to take turns buying an item from a classroom store.  It is a good motivation that includes learning and positive reinforcement.