Summary of the Study
A child’s introduction to geometric shapes begins
in infancy with mobiles, books, blocks, puzzles,
sorting toys, and segments on various television
programs. Without direct instruction, young children
form an understanding of what defines a circle,
triangle, and rectangle by observing and
manipulating these basic shapes and identifying
them by name. -(Mary Anne Hannibal)
Link to Game
I really like this math game. It is a fun way for students to learn names of polygons. I would use this together with the class on the smart board and let each student come up, one person at a time, to select two cards. I would keep the same order of students to come up and keep the game going until every word and polygon was matched. This could be done without keeping score of who gets the matches, or with keeping score ( and dividing the class into two teams with students still taking turns).
Another idea is to make cards for traditional matching games that students could play in smaller groups at their desks. I also like the idea of instead of putting only a word or only a shape on the cards, put the shape and the word on each card. A game that used more cards could also include matching colors too (adding more cards of the same shape in different colors, with every card still having a match to find).
CTGE5227 Personal Learning Path Blog
Friday, March 29, 2019
Thursday, March 21, 2019
Hopping on the Number Line
This week, I chose a lesson that focuses on using a number line. I think number lines are a great visual way for kids to see numbers in order and a great tool for learning addition and subtraction. I would also use a number line to show introduce negative numbers to children and show how to add negative and positive numbers.
Number lines are a great reference for students as well and I would have all of my students have a number line on their desks to use as a reference any time.
I like this lesson, because it makes it fun for children when introducing a number line to the class. It allows them to work with their peers. I would also use the questions. I like the questions, because they encourage children to explain their answer and explain their thinking. Also, I would use the questions as a check for understanding in the lesson.
Number lines provide a mental strategy for addition and subtraction. It's easy to think of them as a kind of crutch for the struggling, but not so. Research has shown they're important because they promote good mental arithmetic strategies.https://komodomath.com/us/blog/number-lines-a-guide
A great way to build your children's number sense is to have number lines available for them at home to use on homework, studying for a test, and/or playing games. This visual model is so important for young children to see so they can make a connection to the abstractness of numbers. https://www.scholastic.com/parents/school-success/learning-toolkit-blog/number-lines.html
Hopping on the Number Line
Materials
- Dominoes
- Number lines
- Counters
Instructional Plan
Tell the students that they will find sums using the number line model. Then display a large number line and a 5+4 domino, that is, a domino with 5 spots on the left side and 4 spots on the right. Then demonstrate with a counter how a hop of 5 is taken on the number line. You may wish to encourage students to count aloud as the hop is made. Then make a hop of 4, starting at the place the counter landed. You might choose to have them record what happened using the equation notation 5 + 4 = 9, or to informally describe the moves this way: “If you take a hop of 5 spaces and then a hop of 4 spaces, you land on 9.” You may wish to highlight the fact that in this model, spaces are counted, not points on the number line.

After several trials, put the students in pairs and give each pair some dominoes, a counter, and individual number lines.
Ask the students to take turns moving the counter on the number line to find the sum shown on the domino and recording the hops in pictures and in equation form. Ask them to draw the first hop and write the first numeral in green and the second hop and numeral in red. Encourage the students to predict the sums and to verify their predictions by moving a counter on the number line.
After allowing time for exploration, ask the students to predict the answers to questions such as “If I take a hop of 3 and then a hop of 5, where will I land?” [8.] Now have students make up 2 similar problems on a piece of paper and trade them with a friend. Students should then solve their partners’ problems using the number line. When the pairs have finished, call them together to discuss what they did. Encourage them to use the number line in their explanation. Then ask “If I take a hop of 5 and then a hop of 4, where will I land?" [9.] "How about if I take a hop of 4 and then a hop of 5?" [9.] "Will this work every time?" [Yes.] Encourage them to explore the order property by writing each first addend in green and each second one in red.
Be sure to lead a discussion about the order (commutative) property. You may need to use other examples to illustrate this important property of addition.
As a concluding activity, pose puzzles such as “I am the number you land on when you take a hop of 5 and then a hop of 1. Who am I?” [6.] You may wish to encourage students to create and share similar problems. One or more of these puzzles could be added to their unit portfolios.
Assessments and Extensions
Assessment Options
- The Questions for Students help students focus on the mathematics and aid you in understanding the students’ current level of knowledge and skill with the mathematical concepts of this lesson. You may want to add others that conversations with the students suggest.
- A teacher’s resource, Class Notes, https://www.nctm.org/uploadedFiles/Content/Lessons/Resources/preK-2/355-AS-classnotes.pdf is provided to document your observations about student understanding and skills. You may find the information useful when planning additional learning experiences for individual students or for documenting progress for students with mandated instructional plans.
Extensions
- Ask students, "How is using a number line like measuring? How is it different?"
- Move on to the next lesson, Exploring Adding With Sets.
Questions and Reflections
Questions for Students
1. What number did you land on when you made a 5-hop, then a 3-hop?
[8.]
2. Could you land on the same number if you took a 3-hop first, then a 5-hop? How do you know?
[Yes; 5 + 3 = 8, and 3 + 5 = 8.]
3. What sums did you model with hops? How did you record them?
[Student responses will depend upon the "hops" they performed.]
4. Were any of the sums the same? Why?
[Student responses will depend upon the "hops" they performed.]
5. How would you find the sum of 2 and 5?
[Make a hop of 2, and then a hop of 5, to reach 7.]
6. How would you tell a friend to add on the number line?
[Student responses may vary.]
Teacher Reflection
- Which students counted as they took hops and which moved directly to the number?
- What activities would be appropriate for students who met all the objectives?
- Which students had trouble using the number line? What instructional experiences do they need next?
- Did any children notice a connection with measurement?
- What adjustments would you make the next time that you teach this lesson?
Objectives and Standards
Learning Objectives
Students will:
- See the number line model to find sums.
- Investigate the order (commutative) property of addition.
- Solve and create puzzles using the number line.
Pre K to 2nd
- Kindergarten
- CCSS.Math.Practice.MP1
Make sense of problems and persevere in solving them. - CCSS.Math.Practice.MP4
Model with mathematics. - CCSS.Math.Practice.MP5
Use appropriate tools strategically. - CCSS.Math.Practice.MP6
Attend to precision.
Pre K to 2nd
- Grade 1
- CCSS.Math.Practice.MP1
Make sense of problems and persevere in solving them. - CCSS.Math.Practice.MP4
Model with mathematics. - CCSS.Math.Practice.MP5
Use appropriate tools strategically. - CCSS.Math.Practice.MP6
Attend to precision.
Pre K to 2nd
- Grade 2
- CCSS.Math.Practice.MP1
Make sense of problems and persevere in solving them. - CCSS.Math.Practice.MP4
Model with mathematics. - CCSS.Math.Practice.MP5
Use appropriate tools strategically. - CCSS.Math.Practice.MP6
Attend to precision.
- CCSS.Math.Practice.MP1
Make sense of problems and persevere in solving them.
- CCSS.Math.Practice.MP4
Model with mathematics.
- CCSS.Math.Practice.MP5
Use appropriate tools strategically.
- CCSS.Math.Practice.MP6
Attend to precision.
Related Resources
 |
Grade: PreK to 2nd
Focuses on the counting model for addition using literature and dominoes.
|
 |
Grade: PreK to 2nd
Use sets to explore addition properties. |
 |
Grade: PreK to 2nd
Use the balance model of addition. |
 |
Grade: PreK to 2nd
Use dominoes to find doubles for addition. |
 |
Grade: PreK to 2nd
Relate addition and subtraction. |
Friday, March 15, 2019
This week I chose to explore a lesson that involves sorting. I think this is a great way to introduce sorting to children and connect it to math. I would use this lesson also as a way to encourage working together and sharing ideas. I like how when the children are going to sort the crayons by color, size, type, and shape, the lesson notes that children might interpret the categories differently, and use this as an opportunity to engage in math talk.
Another thing I like about this lesson is that it suggests that students will need "multiple sorting experiences" in the early grades. I think in addition to teaching and talking about "how to sort", it would be fun to make bins of items to be sorted, that children can access in the classroom. During free time, children could pick a bin, take it to his/her desk, and look/touch the items and let practice sorting other items by color, size, type, and shape.
Properties Everywhere
Materials
- Chart paper
- Small bowls for each working group
- Crayons or pencils (or a small alternative) to sort
- Objects to Sort Recording Sheet
Instructional Plan
While students remain in their seats, ask them to identify things within the classroom that can be sorted and to name specific attributes to guide the sorting. Some examples students might suggest are the following:
- Things to sort by color: crayons, markers, papers, hair color, eye color, backpacks, and clothes
- Things to sort by shape: tables, books, blocks
- Things to sort by size: books, students, pencils, and shoes.
Record and post this information on a chart for future reference. The format provided on the Objects to Sort Recording Sheet will familiarize students with the recording format.
Give small groups of students bowls of crayons or pencils. Have students sort the crayons however they wish (be vague on purpose, so that the groups' results will vary). While students are doing this, circulate the room and make note of all the different ways groups are sorting.

After students have finished sorting, display one group's sorting results. Ask the class if they can guess how this group sorted their objects. Have students defend their answers.
https://www.nctm.org/uploadedFiles/Content/Lessons/Resources/preK-2/271-AS-ObjectSort.pdf
Distribute the Objects to Sort Recording Sheet (one copy per group). Invite students to complete the sheet by using more specific sorting rules. Students will have to sort the crayons by such the following categories:
- Color (they can mark the crayon onto the paper)
- Size (students may use length, width, or both)
- Type (ex: crayons with and without wrapping)
- Shape (ex: crayons with tips vs. those that resemble cylindrical cylinders)
Note that students may interpret the categories differently, which is acceptable. This will be a good opportunity to engage students in math talk.
Depending on the time available for class, use the Questions for Students to wrap up the lesson, or move onto the next lesson, Alike and Different.
Assessments and Extensions
Assessments
- The guiding questions help students focus on the mathematics and aid you in understanding the students’ level of knowledge and skill with the mathematical concepts of this lesson.
- One of the assessment tools provided is a recording sheet entitled Class Notes. It is helpful to record students’ current level of understanding as a way to plan instruction and to monitor and measure their growth toward meeting the learning objectives. Documenting information about students’ understanding throughout the lesson can help you focus on each student’s needs and strengths and thus increase students’ learning opportunities.
 Class Notes
Class Notes - https://www.nctm.org/uploadedFiles/Content/Lessons/Resources/ClassNotes.pdf
Extensions
- Many students in the early grades will need multiple sorting experiences. You may wish to ask students to use these procedures as they sort other objects such as small toys, models of vegetables or fruits, jewelry, keys, tops for containers, bread clips, and coins.
- Have students think about other categories that they can sort by. For example, people can be sorted by gender, eye color, hair color, etc.
Questions and Reflections
Questions for Students
[All answers will vary.]
- What kinds of shoes do you have at your house? (Encourage students to look at their own shoes and think about shoes they have at home such as dress shoes, mom’s high-heeled shoes, basketball shoes, slippers, and sandals.)
- What was your rule for sorting? Why did you choose it?
- Could you use one other rule that is different from the one you used?
- Could you use more than one property or attribute for sorting?
- What things could you sort at home? (Students might name toys, clothes, groceries, shoes, etc.)
- Do you sort objects at home by where they belong? If so, where? Answers might include the pantry, drawers, toy chest, and so forth.
Teacher Reflection
- Which management strategies were most effective?
- Which management strategies were least effective?
- Which students met all the objectives of this lesson? What extension activities are appropriate for those students?
- Which students did not meet the objectives of this lesson? What instructional experiences do they need next? What mathematical ideas need clarification?
- What adjustments would you make the next time you teach this lesson?
Objectives and Standards
Learning Objectives
Students will:
- Identify how items are sorted by color, size, type and shape.
- Defend their reasoning for sorting.
Pre K to 2nd
- Kindergarten
- CCSS.Math.Practice.MP7
Look for and make use of structure. - CCSS.Math.Practice.MP8
Look for and express regularity in repeated reasoning.
Pre K to 2nd
- Grade 1
- CCSS.Math.Practice.MP7
Look for and make use of structure. - CCSS.Math.Practice.MP8
Look for and express regularity in repeated reasoning.
Pre K to 2nd
- Grade 2
- CCSS.Math.Practice.MP7
Look for and make use of structure. - CCSS.Math.Practice.MP8
Look for and express regularity in repeated reasoning.
- CCSS.Math.Practice.MP7
Look for and make use of structure.
- CCSS.Math.Practice.MP8
Look for and express regularity in repeated reasoning.
Related Resources
 |
Grade: PreK to 2nd
Identify properties, and sort, classify, organize, and display data. |
 |
Grade: PreK to 2nd
Students compare objects to build ideas about variables.
|
|
Grade: PreK to 2nd
Model how to organize data and use the vocabulary associated with collecting, organizing, and displaying data.
| |
.png) |
Grade: PreK to 2nd
Describe graphs using appropriate vocabulary, and develop skills in posing and responding to questions about graphs. |
Friday, March 8, 2019
Eggsactly with a Dozen Eggs
This week, I chose to explore this lesson, "Eggsactly with a Dozen Eggs." The materials needed are simple and cost effective. Something I would do is incorporate the model on the classroom smart board also with eggs that can be virtually moved inside and outside the carton. To encourage mathematical discourse, first I would assign students to working in pairs. Then I would ask them to talk to the group next to them and share their ideas after completing each question on the worksheet. This will get the students more comfortable with working with classmates and become more comfortable with mathematical discourse. Also the students learn from each other. Then students could come up to the smart board and show their answers. This would give me the opportunity to ask, "How did you know that? or What other fractions are equivalent?"
Another thing I like about this lesson is when doing the worksheet, if I the class talked about and shared answers on the smart board for one question at a time, it is easy to do in more than one math session. For example if Day one, we did the lesson and stopped after question number one, on day two it would be easy to pick up where we left off. If needed, a quick review of the question the students did the previous day could be done before moving on. Or, the students could just pick up where they left off the day before. Overall, I think the lesson has a nice flow and would interest the students.
Eggsactly with a Dozen Eggs
Materials
- An egg carton filled with 12 plastic eggs (or 12 markers) for each pair of students
- Eggsactly Eggs Activity Sheet
Instructional Plan
Introduce the set representation by having each pair of students examine an egg carton filled with plastic eggs (or some other marker if plastic eggs are unavailable or cost prohibitive.) Ask students how many eggs are in the set. [12.] Suppose six are used to bake a cake. Have students remove six eggs. Students should record their egg configuration on the Eggsactly Eggs Activity Sheet.
Have students participate in a gallery walk examining other students’ egg cartons to see all the different ways students might have removed six.
- Ask students what all the egg cartons have in common. [There are six remaining.]
- What fraction of the entire set is 6? [6/12; accept 1/2 or other equivalent fractions.] If students do not make the connection between equivalent fractions, e.g., 6/12 = ___, they have an opportunity to develop these relationships in later lessons.
- What fraction was removed? [6/12 or 1/2] Have students label their recording sheet as 6/12. Some students may choose to label their sheet with an equivalent fraction, such as 1/2. If so, this provides an excellent opportunity to introduce equivalent fractions.

Continue removing varying numbers of eggs. For example, suppose this time that we need eight eggs to bake our cake. Have students remove eight eggs. Students should record their egg configuration on the Eggsactly Eggs Activity Sheet. Have students go on another gallery walk to see all the different ways students might have removed eight.
- Ask students what all the egg cartons have in common. [There are four remaining.]
- What fraction of the entire set is 4? [4/12; accept 1/3 or 2/6.]
- What fraction was removed? [8/12, 2/3, or 4/6.] For the remaining eggs, have students label their recording sheet as 4/12. [Accept 1/3 or 2/6.]
Have students investigate the different ways they can arrange their eggs when given the fraction. For example, ask students to show 1/4 of a dozen? (Use the Eggsactly Eggs Activity Sheet to have students represent several different configurations all equivalent to 1/4 of a dozen.) Have students identify fraction relationships associated with the set (e.g., 6 of the set of 12 eggs is the same as 6/12 of the set, OR when the numerator stays the same and the denominator increases, the fractions become smaller — 1/3 is smaller in area than 1/2).
Have students work in pairs to continue the investigation as different numbers of eggs are used. Students should be given time to investigate the variety of ways in which the eggs can be arranged. These arrangements should be recorded on the Eggsactly Eggs Activity Sheet and the sheet should be labeled according to the fraction. For example, students might use several images of the egg carton on the activity sheet to record all the ways to show x of a dozen.
Have students investigate the different ways they can arrange their eggs when given the fraction. For example, ask students to show 1/4 of a dozen? (Use the Eggsactly Eggs Activity Sheet to have students represent several different configurations all equivalent to 1/4 of a dozen.) Have students identify fraction relationships associated with the set (e.g., 1/2 of the set of 12 eggs is the same as 6/12 of the set, OR when the numerator stays the same and the denominator increases, the fractions become smaller, e.g. 1/3 is smaller in area than 1/2).
Convene the whole class to discuss the activities in this lesson. The guiding questions may be used to focus the class discussion as they were used to focus individual student’s attention on the mathematics learning objectives of this lesson.
Assessments and Extensions
Assessment Option
- At this stage of the unit, it is important to know whether students can:
- Demonstrate understanding that a fraction can be represented as part of a set
- Identify fractions when the whole (set) and part of the set are given
- Identify fraction relationships associated with a set of twelve
- Student recordings can be used to make instructional decisions about students’ understanding of fraction relationships. Areas needing additional work can be developed during subsequent lessons. More challenging experiences can be provided for those students who need them. You may choose to use the Class Notes recording sheet to make anecdotal notes about students’ understandings.
- Collect students' Eggsactly Eggs Activity Sheets. Use the Eggsactly Eggs Answer Key to check student responses to the questions on the activity sheet.
 Eggsactly Eggs Answer Key
Eggsactly Eggs Answer Key Answer Key
Extension
Move on to the next lesson, Eggsactly with Eighteen Eggs.
Questions and Reflections
Questions for Students
1. What do you notice about the relationship between 1/2 of a dozen and 1/4 of a dozen?
[Students should be able to tell from their recordings that 1/4 is half of 1/2.]
2. What do you notice about the relationship between 1/3 of a dozen and 1/6 of a dozen?
[Students should be able to tell from their recordings that 1/6 is half of 1/3.]
3. What can you tell about the size of the fraction when the numerator is the same for both fractions, e.g., 1/4 and 1/6?
[The smaller the denominator, the larger the fraction.]
4. What can you tell about the size of the fraction when the denominator is the same for both fractions, e.g. 2/5 and 3/5?
[The smaller the numerator, the smaller the fraction.]
Teacher Reflection
- Which students understand that a fraction can be represented as part of a set? What activities are appropriate for students who have not yet developed this understanding?
- Which students can identify fractions when the whole (set) and part of the set is given? What activities are appropriate for students who have not yet developed this understanding?
- Which students/groups can articulate relationships between fractions?
- What parts of the lesson went smoothly? What parts should be modified for the future?
Objectives and Standards
Learning Objectives
Students will:
- Demonstrate understanding that a fraction can be represented as part of a set, given a set of identical items (eggs).
- Identify fractions when the whole (set) and part of the set is given.
- Identify fraction relationships associated with the set, such as one fourth is one half of one half.
3rd to 5th
- Grade 3
- CCSS.Math.Practice.MP4
Model with mathematics. - CCSS.Math.Practice.MP5
Use appropriate tools strategically.
3rd to 5th
- Grade 4
- CCSS.Math.Practice.MP4
Model with mathematics. - CCSS.Math.Practice.MP5
Use appropriate tools strategically.
3rd to 5th
- Grade 5
- CCSS.Math.Practice.MP4
Model with mathematics. - CCSS.Math.Practice.MP5
Use appropriate tools strategically.
- CCSS.Math.Practice.MP4
Model with mathematics.
- CCSS.Math.Practice.MP5
Use appropriate tools strategically.
Related Resources
 |
Grade: 3rd to 5th
Examine relationships among the fractions used to describe part of a set of eighteen. |
.jpg) |
Grade: 3rd to 5th
Explore equivalent fractions. |
 |
Grade: 3rd to 5th
Use fractions to describe a set of attribute pieces. |
 |
Grade: 3rd to 5th
Conduct a class survey. |
 |
Grade: 3rd to 5th
Use everyday items to identify fractions. |
Saturday, March 2, 2019
Running Distances
This week, I decided to look at a different topic. As a runner of track and cross country from 1995-1999 I have always appreciated the math involved in calculating distances. Most running events are measured in meters and tracks are measured in meters. This is a unique and fun math topic that could be used a variety of ways.
First some basic information:
400 meters is one lap on an outdoor track
400 meters=.25 Miles
800 meters=.5 Miles
1600 meters=1 mile
5 Kilometers= 3.125 miles
10 Kilometers=6.25 miles
Some questions:
If a runner ran two track events a 1600 meter race and an 800 meter race, how many miles did the runner run? The runner ran a total of 1.5 miles.
A runner ran a total of one mile. If the track events were 400 meters, 800 meters, 1600 meters, 5K, and 10K, what combinations of events could the runner have ran? (The runner could run twice in the same event.) The runner could have ran the 400 meter race four times. The runner could have ran two 400 meter races and one 800 meter race. The runner could have ran two 800 meter races. The runner could have also ran one 1600 meter race.
A runner ran two laps on an outdoor track. What percentage of two miles did the runner run? How could that be represented with a fraction? Two laps is equal to a half mile since each lap is 400 meters and 400 meters is equal to .25 miles. Two miles would be 8 laps on the outdoor track. One half mile is 2 laps. The fraction could be represented by 2/8 or 1/4 or 25%.
A runner was being timed for the 1600 meter race. Lap one was 80 seconds, lap two was 80 seconds, lap 65 seconds. The runner crossed the finish line at exactly 4 minutes and 45 seconds. What was the runners time for lap 4? The first three added up to 3 minutes 45 seconds, so the last lap must have been exactly 60 seconds.
A runner wants to run a mile in 8 minutes on a track and runs a consistent pace that remains the same. Lap one takes the runner 2 minutes. Lap two takes the runner 2 minutes. Is the runner running a pace to run a mile in 8 minutes on an outdoor track? Yes. Four laps of 400 meters each equals a mile (1600 meters) If the runner ran 4 laps, each lap taking 2 minutes, the runner's mile time would be 8 minutes.
A runner is following a training program that is four days per week. The weekly goal is to run 20 kilometers per week, without running more than 10 kilometers in any given day. The runner runs 2 kilometers on day one, 8 kilometers on day two, and 9 kilometers on day. The runner wants to run 10 kilometers on day 4. If the runner runs 10 kilometers on day four, how many kilometers did the runner exceed the goal for that week? The runner ran a total of 29 kilometers that week and exceeded the goal of 20 kilometers by 9 kilometers.
A runner is running a 3200 meter race. The runner just completed lap number six. Write a fraction that represents the amount of the race that the runner has completed so far. 3200 meters would be 8 laps. The runner has completed 6/8 or 3/4 of the race.
A topic like this could also be incorporated into making graphs. For example you could give students information and ask them to create their own graphs...
Example: In a track meet, Sally ran a 3200 meter event, a 1600 meter event, and an 800 meter event. Bob ran a 400 meter event and an 800 meter event. Jeff ran an 800 meter event and a 1600 meter event. Make a graph that represents the total distance each runner ran.
Another way to explore the topic: Ask kids to create: Give them a broad topic such as You are the coach and have ten team members. If there was a limit of each member to run in no more than three events and you had two members that only wanted to run one event each...
The events are the 100 meter race, the 200 meter race, 400 meter race, the 800 meter race, the 1600 meter race, and the 3200 meter race. Do you have enough team members to have two people in each race? Yes. There are a total of six events. You have ten team members. Ask them to draw out their schedule of what team members are scheduled in each event. Team members could be represented by Member A and Member B (for the team members that only want to run one event) and Members 1-8 who can run up to three events.
Then after this is complete and they have drawn up their schedule, ask a variable question such as "Now Members 1 and 2 ask to be in the 400 meter race." Can you accommodate their request and still have team members in every event? If so, how?
The Team scenario is could be kind of tricky so I would use it if the group was ready for it and walk and talk them through a similar example on a smart board first. This is a fun topic that could be altered or modified if needed.
First some basic information:
400 meters is one lap on an outdoor track
400 meters=.25 Miles
800 meters=.5 Miles
1600 meters=1 mile
5 Kilometers= 3.125 miles
10 Kilometers=6.25 miles
Some questions:
If a runner ran two track events a 1600 meter race and an 800 meter race, how many miles did the runner run? The runner ran a total of 1.5 miles.
A runner ran a total of one mile. If the track events were 400 meters, 800 meters, 1600 meters, 5K, and 10K, what combinations of events could the runner have ran? (The runner could run twice in the same event.) The runner could have ran the 400 meter race four times. The runner could have ran two 400 meter races and one 800 meter race. The runner could have ran two 800 meter races. The runner could have also ran one 1600 meter race.
A runner ran two laps on an outdoor track. What percentage of two miles did the runner run? How could that be represented with a fraction? Two laps is equal to a half mile since each lap is 400 meters and 400 meters is equal to .25 miles. Two miles would be 8 laps on the outdoor track. One half mile is 2 laps. The fraction could be represented by 2/8 or 1/4 or 25%.
A runner was being timed for the 1600 meter race. Lap one was 80 seconds, lap two was 80 seconds, lap 65 seconds. The runner crossed the finish line at exactly 4 minutes and 45 seconds. What was the runners time for lap 4? The first three added up to 3 minutes 45 seconds, so the last lap must have been exactly 60 seconds.
A runner wants to run a mile in 8 minutes on a track and runs a consistent pace that remains the same. Lap one takes the runner 2 minutes. Lap two takes the runner 2 minutes. Is the runner running a pace to run a mile in 8 minutes on an outdoor track? Yes. Four laps of 400 meters each equals a mile (1600 meters) If the runner ran 4 laps, each lap taking 2 minutes, the runner's mile time would be 8 minutes.
A runner is following a training program that is four days per week. The weekly goal is to run 20 kilometers per week, without running more than 10 kilometers in any given day. The runner runs 2 kilometers on day one, 8 kilometers on day two, and 9 kilometers on day. The runner wants to run 10 kilometers on day 4. If the runner runs 10 kilometers on day four, how many kilometers did the runner exceed the goal for that week? The runner ran a total of 29 kilometers that week and exceeded the goal of 20 kilometers by 9 kilometers.
A runner is running a 3200 meter race. The runner just completed lap number six. Write a fraction that represents the amount of the race that the runner has completed so far. 3200 meters would be 8 laps. The runner has completed 6/8 or 3/4 of the race.
A topic like this could also be incorporated into making graphs. For example you could give students information and ask them to create their own graphs...
Example: In a track meet, Sally ran a 3200 meter event, a 1600 meter event, and an 800 meter event. Bob ran a 400 meter event and an 800 meter event. Jeff ran an 800 meter event and a 1600 meter event. Make a graph that represents the total distance each runner ran.
Another way to explore the topic: Ask kids to create: Give them a broad topic such as You are the coach and have ten team members. If there was a limit of each member to run in no more than three events and you had two members that only wanted to run one event each...
The events are the 100 meter race, the 200 meter race, 400 meter race, the 800 meter race, the 1600 meter race, and the 3200 meter race. Do you have enough team members to have two people in each race? Yes. There are a total of six events. You have ten team members. Ask them to draw out their schedule of what team members are scheduled in each event. Team members could be represented by Member A and Member B (for the team members that only want to run one event) and Members 1-8 who can run up to three events.
Then after this is complete and they have drawn up their schedule, ask a variable question such as "Now Members 1 and 2 ask to be in the 400 meter race." Can you accommodate their request and still have team members in every event? If so, how?
The Team scenario is could be kind of tricky so I would use it if the group was ready for it and walk and talk them through a similar example on a smart board first. This is a fun topic that could be altered or modified if needed.
Thursday, February 21, 2019
Tasks, Questions, and Practices
Tasks, Questions, and Practices
By Chandra Hawley Orrill, Posted May 11, 2015 –
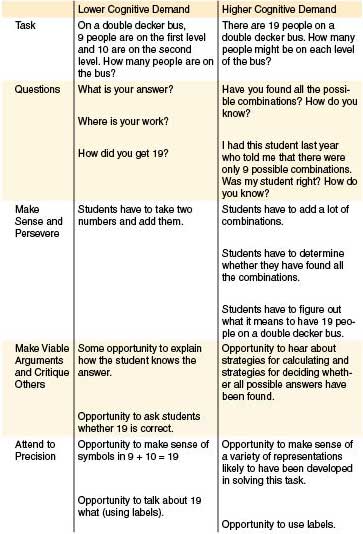
We know that to understand how our students think, we need to ask them good questions. We read all the time about the importance of questioning and different kinds of questions. But, all questions are not created equally. In this two-part blog entry, I want to explore the relationship among asking questions, the problems we use in our classrooms, and the effects questions and tasks have on our ability to address some of the Common Core’s Standards for Mathematical Practice (CCSSI 2010). Specifically, let’s think about these Standards of Practice:
SMP 1. Make sense of problems and persevere in solving them
SMP 6. Construct viable arguments and critique the reasoning of others.
SMP 3. Attend to precision.
The goal of this blog post is to emphasize the point that the tasks you choose to use in your classroom enhance or inhibit your ability to ask the kinds of questions that allow students to develop these three Standards for Mathematical Practice (SMPs).
By Chandra Hawley Orrill, Posted May 11, 2015 –
We know that to understand how our students think, we need to ask them good questions. We read all the time about the importance of questioning and different kinds of questions. But, all questions are not created equally. In this two-part blog entry, I want to explore the relationship among asking questions, the problems we use in our classrooms, and the effects questions and tasks have on our ability to address some of the Common Core’s Standards for Mathematical Practice (CCSSI 2010). Specifically, let’s think about these Standards of Practice:
SMP 1. Make sense of problems and persevere in solving them
SMP 6. Construct viable arguments and critique the reasoning of others.
SMP 3. Attend to precision.
The goal of this blog post is to emphasize the point that the tasks you choose to use in your classroom enhance or inhibit your ability to ask the kinds of questions that allow students to develop these three Standards for Mathematical Practice (SMPs).
Tasks Matter
The cognitive demand of a task is the level of cognitive engagement needed to complete the task (Stein et al. 2009). You could think of a problem that requires only memorization as being at the low end of cognitive demand, whereas a task that requires students to make connections between and among mathematical ideas in new ways is a high cognitive demand task. Research has shown that using high cognitive demand tasks in ways that support that rigor will lead to increases in student learning.
The cognitive demand of a task is the level of cognitive engagement needed to complete the task (Stein et al. 2009). You could think of a problem that requires only memorization as being at the low end of cognitive demand, whereas a task that requires students to make connections between and among mathematical ideas in new ways is a high cognitive demand task. Research has shown that using high cognitive demand tasks in ways that support that rigor will lead to increases in student learning.
Questions Matter
To maintain the level of cognitive demand written into a question, a teacher must ask good questions. A high cognitive demand question is one that invites students to explain their thinking, make new connections, describe their process, or critique other ideas. Questions that maintain high cognitive demand engage students in making more sense of the mathematics, whereas questions that lower the cognitive demand focus on correct answers and correct answer paths.
To maintain the level of cognitive demand written into a question, a teacher must ask good questions. A high cognitive demand question is one that invites students to explain their thinking, make new connections, describe their process, or critique other ideas. Questions that maintain high cognitive demand engage students in making more sense of the mathematics, whereas questions that lower the cognitive demand focus on correct answers and correct answer paths.
Standards of Practice Come from Tasks and Questions
One of the challenges of the Common Core is the need to address the SMPs all the time. We all know that students need to actually practice the SMPs to develop the skills and dispositions that are valued. Although forgetting about the SMPs is easy, they are crucial to students’ development as mathematical thinkers. For this discussion, I’ve chosen three SMPs to focus on because they are all closely related to tasks and questions.
• High cognitive demand tasks require students to make sense of them. Unlike a page of simple number sentences, high cognitive demand tasks require that students read them, determine what the question is, and determine how to use the information provided in the task. Sometimes, this is also true of lower cognitive demand tasks.
• High cognitive demand tasks often have multiple ways of finding an answer or multiple correct answers. When this is true, you and your students have much more to talk about. And many more student ideas come out in the conversation. All of this offers an opportunity to make sense of one another’s thinking and for each student to learn how to communicate about her or his own thinking.
• When we engage in meaningful discussions of mathematics that feature a lot of different ideas, it becomes more and more important to be sure everyone in the room knows exactly what each person is talking about. Precision is developed by being asked to make sure everyone understands a viewpoint. It comes from the use of specific mathematical terms, from labeling answers, and from using representations as tools to support communication about mathematics.
One of the challenges of the Common Core is the need to address the SMPs all the time. We all know that students need to actually practice the SMPs to develop the skills and dispositions that are valued. Although forgetting about the SMPs is easy, they are crucial to students’ development as mathematical thinkers. For this discussion, I’ve chosen three SMPs to focus on because they are all closely related to tasks and questions.
• High cognitive demand tasks require students to make sense of them. Unlike a page of simple number sentences, high cognitive demand tasks require that students read them, determine what the question is, and determine how to use the information provided in the task. Sometimes, this is also true of lower cognitive demand tasks.
• High cognitive demand tasks often have multiple ways of finding an answer or multiple correct answers. When this is true, you and your students have much more to talk about. And many more student ideas come out in the conversation. All of this offers an opportunity to make sense of one another’s thinking and for each student to learn how to communicate about her or his own thinking.
• When we engage in meaningful discussions of mathematics that feature a lot of different ideas, it becomes more and more important to be sure everyone in the room knows exactly what each person is talking about. Precision is developed by being asked to make sure everyone understands a viewpoint. It comes from the use of specific mathematical terms, from labeling answers, and from using representations as tools to support communication about mathematics.
Your Turn
Now it’s your turn to think about the effects of Tasks, Questions, and Practices. Consider the two tasks below.
1. Decide which aspects of each task make them of higher or lower cognitive demand. Could you do anything to raise the cognitive demand of either task?
2. Think about questions you could ask students as they work on these tasks. Are these questions raising or lowering the cognitive demand of the task?
3. How does each task attend to perseverance and sense making?
4. How does each task promote making viable arguments? What about critiquing the arguments of others?
5. How does each task provide students with opportunities to communicate in precise ways about mathematics?
Now it’s your turn to think about the effects of Tasks, Questions, and Practices. Consider the two tasks below.
1. Decide which aspects of each task make them of higher or lower cognitive demand. Could you do anything to raise the cognitive demand of either task?
2. Think about questions you could ask students as they work on these tasks. Are these questions raising or lowering the cognitive demand of the task?
3. How does each task attend to perseverance and sense making?
4. How does each task promote making viable arguments? What about critiquing the arguments of others?
5. How does each task provide students with opportunities to communicate in precise ways about mathematics?
Task 1. Lunchroom Problem
Ella would like to buy lunch in the lunchroom today. Meals cost $2.50. Dessert costs an extra 75 cents, and milk costs 75 cents. If Ella has $5.00, can she buy lunch in the lunchroom? (Please See Chart at the bottom of this post.)
Ella would like to buy lunch in the lunchroom today. Meals cost $2.50. Dessert costs an extra 75 cents, and milk costs 75 cents. If Ella has $5.00, can she buy lunch in the lunchroom? (Please See Chart at the bottom of this post.)
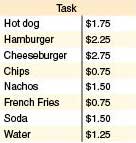
Task 2. Buying Lunch
You are going to the amusement park. At the amusement park, you will buy lunch. You don’t want to carry coins, only dollar bills, because coins can fall out of your pocket on the roller coaster. You can purchase any of the items on the menu, but you cannot buy more than one of the same item, and you cannot spend more than $10.00. Using the menu to the left, find out how many different lunches you could buy without receiving any change back.
You are going to the amusement park. At the amusement park, you will buy lunch. You don’t want to carry coins, only dollar bills, because coins can fall out of your pocket on the roller coaster. You can purchase any of the items on the menu, but you cannot buy more than one of the same item, and you cannot spend more than $10.00. Using the menu to the left, find out how many different lunches you could buy without receiving any change back.
More Reading about Cognitively Demanding Mathematical Tasks
National Council for Teachers of Mathematics. 2014. Principles to Action: Ensuring Mathematical Success for All. Reston, VA: National Council of Teachers of Mathematics.
Common Core State Standards Initiative. CCSSI. 2010. Common Core State Standards for Mathematics (CCSSM). Washington, DC: National Governors Association Center for Best Practices and the Council of Chief State School Officers. http://www.corestandards.org/wp-content/uploads/Math_Standards.pdf
Stein, Mary Kay, Margaret Schwan Smith, Marjorie A. Henningsen, and Edward A. Silver. 2009. Implementing Standards-Based Mathematics Instruction: A Casebook For Professional Development, 2nd ed. New York: Teachers College Press.
 Chandra Hawley Orrill, corrill@umassd.edu, is an associate professor and department chairperson in STEM Education and Teacher Development at the University of Massachusetts–Dartmouth. She teaches courses on mathematics content, like proportional reasoning and number sense, for teachers seeking their professional license as well as teaching a variety of courses in the Mathematics Education PhD program. Her interest is in how teachers understand the mathematics they teach and how we can better support teachers in understanding mathematics. She has conducted hundreds of hours of professional development focused on standards-based mathematics and on technology integration in mathematics for elementary school teachers.
Chandra Hawley Orrill, corrill@umassd.edu, is an associate professor and department chairperson in STEM Education and Teacher Development at the University of Massachusetts–Dartmouth. She teaches courses on mathematics content, like proportional reasoning and number sense, for teachers seeking their professional license as well as teaching a variety of courses in the Mathematics Education PhD program. Her interest is in how teachers understand the mathematics they teach and how we can better support teachers in understanding mathematics. She has conducted hundreds of hours of professional development focused on standards-based mathematics and on technology integration in mathematics for elementary school teachers.
This week, I chose to explore high cognitive demand tasks vs. low cognitive demand tasks. I think it is important for children to make connections with the math they are doing. The more the students make connections the more they will appreciate math and keep a growth mindset.
When completing my assignment Problem Set#1, number 8 sparked my interest: Identify the following task as a "low level" or a "high level" cognitive demand task. If the task is considered a "low level" cognitive demand task, rewrite the task so it is a "high level" cognitive demand task.
Solve. 14+___=21
I determined it was a "low level" cognitive demand task, because it is strictly procedural.
I rewrote it:
Blake has merchandise to sell:
2 Salt Lamps
1 Lava Lamp
2 LED Light Bulbs
2 Regular Light Bulbs
Prices:
Salt Lamps cost $21 each
Lava Lamps cost $14 each
LED Light Bulbs cost $7 each
Light Bulbs cost $2 each
Blake sold $21 worth of merchandise. One item sold was a lava lamp. What did he sell with the lava lamp? (1 LED Light bulb)
Going further, I thought of expanding it.
What merchandise and how many of each remained after the $21 dollar sale?
(2 Salt Lamps, 1 LED Light Bulb and 2 Regular Light Bulbs)
In Blake's final sale, he sells all of the remaining merchandise. How much money was needed to purchase all of the merchandise that was left? ($53)
National Council for Teachers of Mathematics. 2014. Principles to Action: Ensuring Mathematical Success for All. Reston, VA: National Council of Teachers of Mathematics.
Common Core State Standards Initiative. CCSSI. 2010. Common Core State Standards for Mathematics (CCSSM). Washington, DC: National Governors Association Center for Best Practices and the Council of Chief State School Officers. http://www.corestandards.org/wp-content/uploads/Math_Standards.pdf
Stein, Mary Kay, Margaret Schwan Smith, Marjorie A. Henningsen, and Edward A. Silver. 2009. Implementing Standards-Based Mathematics Instruction: A Casebook For Professional Development, 2nd ed. New York: Teachers College Press.
 Chandra Hawley Orrill, corrill@umassd.edu, is an associate professor and department chairperson in STEM Education and Teacher Development at the University of Massachusetts–Dartmouth. She teaches courses on mathematics content, like proportional reasoning and number sense, for teachers seeking their professional license as well as teaching a variety of courses in the Mathematics Education PhD program. Her interest is in how teachers understand the mathematics they teach and how we can better support teachers in understanding mathematics. She has conducted hundreds of hours of professional development focused on standards-based mathematics and on technology integration in mathematics for elementary school teachers.
Chandra Hawley Orrill, corrill@umassd.edu, is an associate professor and department chairperson in STEM Education and Teacher Development at the University of Massachusetts–Dartmouth. She teaches courses on mathematics content, like proportional reasoning and number sense, for teachers seeking their professional license as well as teaching a variety of courses in the Mathematics Education PhD program. Her interest is in how teachers understand the mathematics they teach and how we can better support teachers in understanding mathematics. She has conducted hundreds of hours of professional development focused on standards-based mathematics and on technology integration in mathematics for elementary school teachers.
This week, I chose to explore high cognitive demand tasks vs. low cognitive demand tasks. I think it is important for children to make connections with the math they are doing. The more the students make connections the more they will appreciate math and keep a growth mindset.
When completing my assignment Problem Set#1, number 8 sparked my interest: Identify the following task as a "low level" or a "high level" cognitive demand task. If the task is considered a "low level" cognitive demand task, rewrite the task so it is a "high level" cognitive demand task.
Solve. 14+___=21
I determined it was a "low level" cognitive demand task, because it is strictly procedural.
I rewrote it:
Blake has merchandise to sell:
2 Salt Lamps
1 Lava Lamp
2 LED Light Bulbs
2 Regular Light Bulbs
Prices:
Salt Lamps cost $21 each
Lava Lamps cost $14 each
LED Light Bulbs cost $7 each
Light Bulbs cost $2 each
Blake sold $21 worth of merchandise. One item sold was a lava lamp. What did he sell with the lava lamp? (1 LED Light bulb)
Going further, I thought of expanding it.
What merchandise and how many of each remained after the $21 dollar sale?
(2 Salt Lamps, 1 LED Light Bulb and 2 Regular Light Bulbs)
In Blake's final sale, he sells all of the remaining merchandise. How much money was needed to purchase all of the merchandise that was left? ($53)

Subscribe to:
Comments (Atom)
Pair Matching Polygons
S ummary of the Study A child’s introduction to geometric shapes begins in infancy with mobiles, books, blocks, puzzles, sorting toys, an...

-
This week, I chose a lesson that focuses on using a number line. I think number lines are a great visual way for kids to see numbers in or...
-
This week I chose to explore a lesson that involves sorting. I think this is a great way to introduce sorting to children and connect it t...
-
Exploring Pennies and Dimes Unit: Number Cents Grade: PreK to 2nd Periods: 1 Author: Grace M. Burton Materials Plastic bags, ea...